Published : 26 Sep 2022 07:03 PM
Last Updated : 26 Sep 2022 07:03 PM
டி.என்.பி.எஸ்.சி குரூப் 1 தேர்வு பயிற்சிக்கான எளிய முறை குறிப்புகள் - பகுதி 3
ஜி.கோபாலகிருஷ்ணன், போட்டித்தேர்வு பயிற்சியாளர், குளோபல் விக்கிமாஸ்டர்
தமிழ்நாடு அரசு பணியாளர் தேர்வாணையம் (டி.என்.பி.எஸ்.சி) நடத்தும் குரூப் 1 தேர்வுகள் நவம்பர் 19 அன்று நடத்தப்பட இருக்கின்றன. குரூப்-1 தேர்வுக்கு தயார்செய்துவரும் போட்டியாளர்கள், மாணவர்களுக்கு உதவும் வகையில் ஒவ்வொரு பாடத்துக்குமான எளிய முறை குறிப்புகளை போட்டித் தேர்வு பயிற்சியாளர், குளோபல் விக்கிமாஸ்டர் ஜி.கோபாலகிருஷ்ணன் தொகுத்தளிக்கிறார். கடந்த வெள்ளிக்கிழமை (23.09.2022) அன்று இந்தத் தொடரின் இரண்டாம் பகுதியில் ‘கணிதம் 2’ என்னும் தலைப்பில் எளிய முறை குறிப்புகள் வெளியாகியிருந்தன. இன்றைய மூன்றாம் பகுதியிலும் கணிதத்துக்கான எளிய முறைக் குறிப்புகள் தொடர்கின்றன.
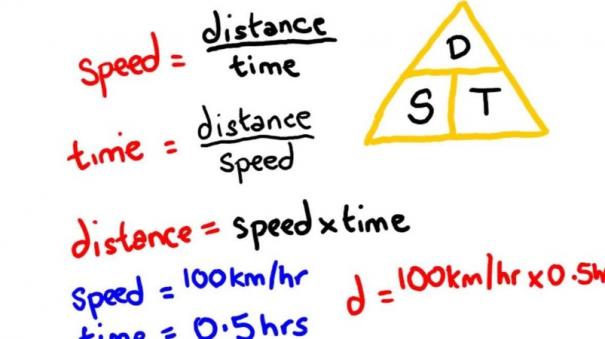
காலமும் தூரமும்
காலமும் தூரமும் கணக்குகளில் நினைவில் நிறுத்தவேண்டியவை.
1 கி.மீ = 1000மீ
1 மணி = 60 நிமிடங்கள்
= 3600 நொடிகள்
1கி.மீ/மணி = 1000மீ/3600நொடி
= (5/18)மீ/நொடி
1மீ/நொடி=(3600/1000 )கி.மீ/மணி
= (18/5)கி.மீ/மணி
மணிவேகம் 'x 'கி.மீ எனில் நொடிவேகம் (5/18)x மீ ஆகும்.
இதே போன்று நொடிவேகம் y மீ எனில் மணிவேகம் (18/5)y கி.மீ ஆகும்.
A, B ஆகிய இரு நபர்கள் சமதூரத்தை x : y வேகத்தில் கடக்கின்றனர் எனில் இருவரும் அத்தூரத்தை கடக்கும் நேரங்களின் விகிதம் y : x ஆகும்.
A, B,C ஆகிய மூன்று நபர்கள் சமதூரத்தை x : y : zவேகத்தில் கடக்கின்றனர் எனில் மூவரும் அத்தூரத்தை கடக்கும் நேரங்களின் விகிதம்
1/x : 1/y : 1/z ஆகும். இதே முறையை நேரங்கள் கொடுத்து வேகங்களை அறியவும் பயன்படுத்தலாம்.
சராசரி வேகம்
ஒரு குறிப்பிட்ட தூரத்தை ஒரு இடத்திலிருந்து 'x' கி.மீ வேகத்தில் சென்றடைந்து திரும்பி கிளம்பிய அதே இடத்திற்கு 'y' கி.மீ வேகத்தில் வந்தடைந்தால் மொத்தப் பயணத்தின் சராசரி வேகம் = 【2xy/(x + y)】கி.மீ. ஆகும்.
பொதுவாக சராசரிவேகம்
= மொத்தம் பயணித்த தூரம் ÷
மொத்த பயணநேரம்
A என்பவர் 'x'கி.மீ /மணி வேகத்தில் 't' மணிநேரமும்
'y' கி.மீ /மணி வேகத்தில் 's' மணிநேரமும் பயணித்தார் எனில் மொத்த பயணத்தின் சராசரி வேகம் (xt + ys)/(t + s) கி.மீ/மணி
புகைவண்டித் தொடர் கணக்குகளில் கவனிக்க வேண்டியவை:
*'l' மீட்டர் நீளமுடைய ஒரு
புகைவண்டித் தொடர் 'x' கி.மீ/மணி வேகத்தில் ஒரு புள்ளியை (ஒரு மரம், ஒரு மின்கம்பம், நிற்கும் ஒரு மனிதன்) கடக்க எடுத்துக்கொள்ளும் நேரம் 't' நொடிகள் எனில் 't' நொடிகளில் கொடுத்துள்ள 'x'கி.மீ வேகத்தில் அவ்வண்டி பயணிக்கும் தூரம் 'l' மீட்டராகும். அதாவது
l = (5/18)xt . இங்குள்ள l, x மற்றும் t ஆகிய மூன்று மாறிகளில் ஏதேனும் இரு மாறிகளின் மதிப்புகள் கொடுக்கப்பட்டடு இருந்தால் மூன்றாவது மதிப்பை மேற்கூறியுள்ள சமன்பாட்டில் பிரதியிட்டு அறியலாம்.
*l' மீட்டர் நீளமுடைய ஒரு
புகைவண்டித் தொடர் 'x' கி.மீ/மணி வேகத்தில் ஒரு குறிப்பிட்ட 'm' மீட்டர் நீளமுடைய ஒரு பாலம் அல்லது நிற்கும் வேறோரு புகைவண்டித்தொடர் அல்லது நடைமேடையைக் கடக்க எடுத்துக்கொள்ளும் நேரம் 't' நொடிகள் எனில் 't' நொடிகளில் கொடுத்துள்ள 'x'கி.மீ வேகத்தில் அவ்வண்டி பயணிக்கும் தூரம்
'l + m' மீட்டராகும். அதாவது
l + m = (5/18)xt . இங்குள்ள l, m, x மற்றும் t ஆகிய நான்கு மாறிகளில் ஏதேனும் மூன்று மாறிகளின் மதிப்புகள் கொடுக்கப்பட்டு இருந்தால் நான்காவது மதிப்பை மேற்கூறியுள்ள சமன்பாட்டில் பிரதியிட்டு அறியலாம்.
**l' மீட்டர் நீளமுடைய ஒரு
புகைவண்டித் தொடர் 'x' கி.மீ/மணி வேகத்திலும் எதிர்திசையிலிருந்து 'y' கி.மீ வேகத்துடன் வரும் 'm' மீட்டர் நீளமுடைய மற்றொரு புகைவண்டித் தொடரும் ஒன்றையொன்று முழுவதுமாக கடக்க எடுத்துக்கொள்ளும் நேரம் 't' நொடிகள் எனில் 't' நொடிகளில் கொடுத்துள்ள வேகங்களின் நெருங்கும் வேகத்தில் அவ்வண்டி பயணிக்கும் தூரம் 'l + m' மீட்டராகும். அதாவது l + m = (5/18)(x + y)t . இங்குள்ள l, m, x , y மற்றும் t - ஐந்து மாறிகளில் ஏதேனும் நான்கு மாறிகளின் மதிப்புகள் கொடுக்கப்பட்டு இருந்தால் ஐந்தாவது மதிப்பை மேற்கூறியுள்ள சமன்பாட்டில் பிரதியிட்டு அறியலாம். இங்கு நெருங்கும் வேகம் ' x + y ' ஆகும்.
* l' மீட்டர் நீளமுடைய ஒரு புகைவண்டித் தொடர் 'x' கி.மீ/மணி வேகத்திலும் அதே திசையிலிருந்து 'y' கி.மீ வேகத்துடன் வரும் 'm' மீட்டர் நீளமுடைய மற்றொரு புகைவண்டித் தொடரும் ஒன்றையொன்று முழுவதுமாகக் கடக்க எடுத்துக்கொள்ளும் நேரம் 't' நொடிகள் எனில் 't' நொடிகளில் கொடுத்துள்ள வேகங்களின் சார்பு வேகத்தில் அவ்வண்டிகள் சேர்ந்து பயணிக்கும் தூரம்
'l + m' மீட்டராகும்.
அதாவது l + m = (5/18)(y - x)t . இங்குள்ள l, m, x , y மற்றும் t - ஐந்து மாறிகளில் ஏதேனும் நான்கு மாறிகளின் மதிப்புகள் கொடுக்கப்பட்டடு இருந்தால் ஐந்தாவது மதிப்பை மேற்கூறியுள்ள சமன்பாட்டில் பிரதியிட்டு அறியலாம். இங்கு y>x ஆக இருப்பின் சார்பு வேகம் 'y - x ' ஆகும். y< x ஆக இருந்தால் சார்பு வேகம் ' x - y ' என எடுத்துக்கொள்ளவேண்டும்.
குறிப்பு : பின்னால் வரும் வண்டியின் வேகம் அதிகமாக இருந்தால்தான் அவ்வண்டி முன்னால் செல்லும் வண்டியை முந்திச் செல்ல இயலும் என்பதை கருத்தில் கொள்ள வேண்டும்.
ஒரே நேரத்தில் புகைவண்டித்தொடர் P, A என்ற இடத்திலிருந்து புறப்பட்டு B ஐ நோக்கி 'x' கி.மீ/மணி வேகத்திலும், புகைவண்டித்தொடர் Q, B என்ற இடத்திலிருந்து புறப்பட்டு A ஐ நோக்கி 'y' கி.மீ/மணி வேகத்திலும் வந்து ஒன்றையொன்று சந்தித்தபின் புகைவண்டித் தொடர் P, B ஐ அடைவதற்கு T மணிகளும்,
புகைவண்டித் தொடர் Q, A ஐ அடைவதற்கு T' மணிகளும் எடுத்துக்கொண்டால் P, Q புகைவண்டித் தொடர்களின் வேகங்களின் விகிதம் அறிய கீழ்க்கண்ட சூத்திரத்தை பயன்படுத்தலாம்.
x : y =√T' : √T
படகு மற்றும் ஓடைக் கணக்குகளில் நிலையான நீரில் படகின் வேகம் x கி.மீ/மணி மற்றும் நீரோட்டத்தின் வேகம் y கி.மீ/மணி என இரு வேகங்கள் கொடுக்கப்பட்டு இருக்கும். நீரோட்டத்துடன் படகின்வேகம் (ds) = (down stream) = (x + y)கி.மீ/மணி
நீரோட்டத்தை எதிர்த்து படகின்வேகம்(us) = (up stream) = (x - y)கி.மீ/மணி.
குறிப்பு : y>x ஆக இருப்பின் படகு நீரோட்டத்தை எதிர்த்துச் செல்ல இயலாது.
நீரோட்டத்துடன் படகின்வேகம் (ds) மற்றும் நீரோட்டத்தை எதிர்த்து படகின்வேகம் (us) கொடுக்கப்பட்டிருந்தால்
நிலையான நீரில் படகின் வேகம் = 【(ds) + (us)】÷ 2
நீரோட்டத்தின் வேகம் = 【(ds) - (us)】÷ 2
ஆறு/ஓடை யின் அகலம் 'w' கி.மீ ஆக இருக்கும்போது ஒரு படகு இக்கரையிலிருந்து அக்கரை சென்று வர 'T' மணிகள் ஆகிறது எனில் படகு பயணித்த மொத்த தூரம் 2w=【2(ds)×(us)】÷ 【(ds) + (us)】× T
இச்சமன்பாட்டில் உள்ள நான்கு மாறிகளில் ஏதேனும் மூன்று மாறிகள் தெரிந்தால் நான்காவது மாறியை கண்டறியலாம்.
இந்தக் கட்டுரையில் கொடுக்கப்பட்டுள்ள எளிய முறைகளை பயன்படுத்தி இத்தலைப்பில் பல கணக்குகள் செய்து பழகவேண்டும்.
(தொடரின் அடுத்த பகுதி செப்டம்பர் 28, புதன்கிழமை அன்று வெளியாகும்)
தொகுப்பு - ஜி.கோபாலகிருஷ்ணன், போட்டித்தேர்வு பயிற்சியாளர், குளோபல் விக்கிமாஸ்டர்
FOLLOW US
தவறவிடாதீர்!
Sign up to receive our newsletter in your inbox every day!



WRITE A COMMENT